作业3 完成

numerical_analysis/3/README.md

@@ -0,0 +1,18 @@
+
+# 问题1
+
+1:
+    f = 1 / (e^(-x) + e^x)
+
+2
+
+标签
+
+    0： 默认求解器
+    1： 向前差分
+    2： 向后差分
+    3： rk45
+
+![image-20210117035636815](https://public.veypi.com/img/screenshot/20210117035636.png)
+
+![image-20210117040727886](https://public.veypi.com/img/screenshot/20210117040727.png)

numerical_analysis/3/main.py

@@ -0,0 +1,153 @@
+import math
+from math import e
+import numpy as np
+import matplotlib.pyplot as plt
+from scipy.integrate import odeint, solve_bvp, solve_ivp
+
+
+def runge_kutta(y, x, dx, f):
+    """ y is the initial value for y
+        x is the initial value for x
+        dx is the time step in x
+        f is derivative of function y(t)
+    """
+    k1 = dx * f(y, x)
+    k2 = dx * f(y + 0.5 * k1, x + 0.5 * dx)
+    k3 = dx * f(y + 0.5 * k2, x + 0.5 * dx)
+    k4 = dx * f(y + k3, x + dx)
+    return y + (k1 + 2 * k2 + 2 * k3 + k4) / 6.
+
+
+'''
+    为了兼容solve_ivp的参数形式，微分方程函数定义的参数顺序为(t,y)，因此使用odeint函数时需要使参数tfirst=True
+    二阶甚至高阶微分方程组都可以变量替换成一阶方程组的形式，再调用相关函数进行求解，因此编写函数的时候，不同于一阶微分方程，二阶或者高阶微分方程返回的是低阶到高阶组成的方程组，
+
+'''
+
+y0 = [1 / (e + 1 / e), (e - 1 / e) / ((e + 1 / e) ** 2)]  # 初值条件
+
+
+# 初值[2,0]表示y(0)=2,y'(0)=0
+
+
+def fvdp1(t, y):
+    '''
+    要把y看出一个向量，y = [dy0,dy1,dy2,...]分别表示y的n阶导，那么
+    y[0]就是需要求解的函数，y[1]表示一阶导，y[2]表示二阶导，以此类推
+    对于二阶微分方程，肯定是由0阶和1阶函数组合而成的，所以下面把y看成向量的话，y0表示最初始的函数，也就是我们要求解的函数，y1表示一阶导，对于高阶微分方程也可以以此类推
+    '''
+    dy1 = y[1]  # y[1]=dy/dt，一阶导
+    # dy2 = -3 * y[1] - 2 * y[0] + np.exp(-1 * t)
+    dy2 = 2 * y[1] ** 2 / y[0] - y[0]
+    # y[0]是最初始，也就是需要求解的函数
+    # 注意返回的顺序是[一阶导， 二阶导]，这就形成了一阶微分方程组
+    return [dy1, dy2]
+
+
+def solve0():
+    '''
+    内置求解器1
+    '''
+    t2 = np.linspace(-1, 1, 1000)
+    return odeint(fvdp1, y0, t2, tfirst=True)[:, 0]
+
+
+def solve01(seq):
+    f0 = [y0[0]]
+    f1 = [y0[1]]
+    f2 = [fvdp1(-1, [f0[0], f1[0]])[1]]
+    for i in range(1, len(seq)):
+        h = seq[i] - seq[i - 1]
+        k21 = f2[i - 1]
+        k22 = fvdp1(seq[i - 1] + h / 2, [f0[i - 1] + h * k21 / 2, f1[i - 1] + h * k21 / 2])[1]
+        k23 = fvdp1(seq[i - 1] + h / 2, [f0[i - 1] + h * k22 / 2, f1[i - 1] + h * k22 / 2])[1]
+        k24 = fvdp1(seq[i - 1] + h / 2, [f0[i - 1] + h * k23, f1[i - 1] + h * k23])[1]
+        f1.append(f1[i - 1] + h * (k21 + k22 + k23 + k24) / 6)
+        f0.append(f0[i - 1] + h * f1[i - 1])
+        f2.append(fvdp1(seq[i], [f0[i], f1[i]])[1])
+    return f0
+
+
+def solve1(seq):
+    '''
+    向前差分
+    '''
+    f0 = [y0[0]]
+    f1 = [y0[1]]
+    f2 = [fvdp1(-1, [f0[0], f1[0]])[1]]
+    for i in range(1, len(seq)):
+        h = seq[i] - seq[i - 1]
+        f0.append(f0[i - 1] + h * f1[i - 1])
+        f1.append(f1[i - 1] + h * f2[i - 1])
+        f2.append(fvdp1(seq[i], [f0[i], f1[i]])[1])
+    return f0
+
+
+def solve2(seq):
+    '''
+    向后差分
+    '''
+    f0 = [y0[0]]
+    f1 = [y0[1]]
+    f2 = [fvdp1(-1, [f0[0], f1[0]])[1]]
+    for i in range(1, len(seq)):
+        h = seq[i] - seq[i - 1]
+        f2.append(fvdp1(seq[i], [f0[i - 1], f1[i - 1]])[1])
+        f1.append(f1[i - 1] + h * f2[i])
+        f0.append(f0[i - 1] + h * f1[i])
+    return f0
+
+
+def runge_kutta(y, x, dx, f):
+    """ y is the initial value for y
+        x is the initial value for x
+        dx is the time step in x
+        f is derivative of function y(t)
+    """
+    k1 = dx * f(y, x)
+    k2 = dx * f(y + 0.5 * k1, x + 0.5 * dx)
+    k3 = dx * f(y + 0.5 * k2, x + 0.5 * dx)
+    k4 = dx * f(y + k3, x + dx)
+    return y + (k1 + 2 * k2 + 2 * k3 + k4) / 6.
+
+
+def solve3(seq):
+    '''
+    rk4
+    '''
+    return solve_ivp(fvdp1, t_span=(-1, 1.0), y0=y0, t_eval=seq).y.T[:, 0]
+
+
+def show():
+    t0 = np.linspace(-1, 1, 1000)
+    r0 = solve0()
+    t1 = np.linspace(-1, 1, 6)
+    r1 = solve1(t1)
+    t2 = np.linspace(-1, 1, 6)
+    r2 = solve2(t2)
+    t3 = np.linspace(-1, 1, 6)
+    r3 = solve3(t3)
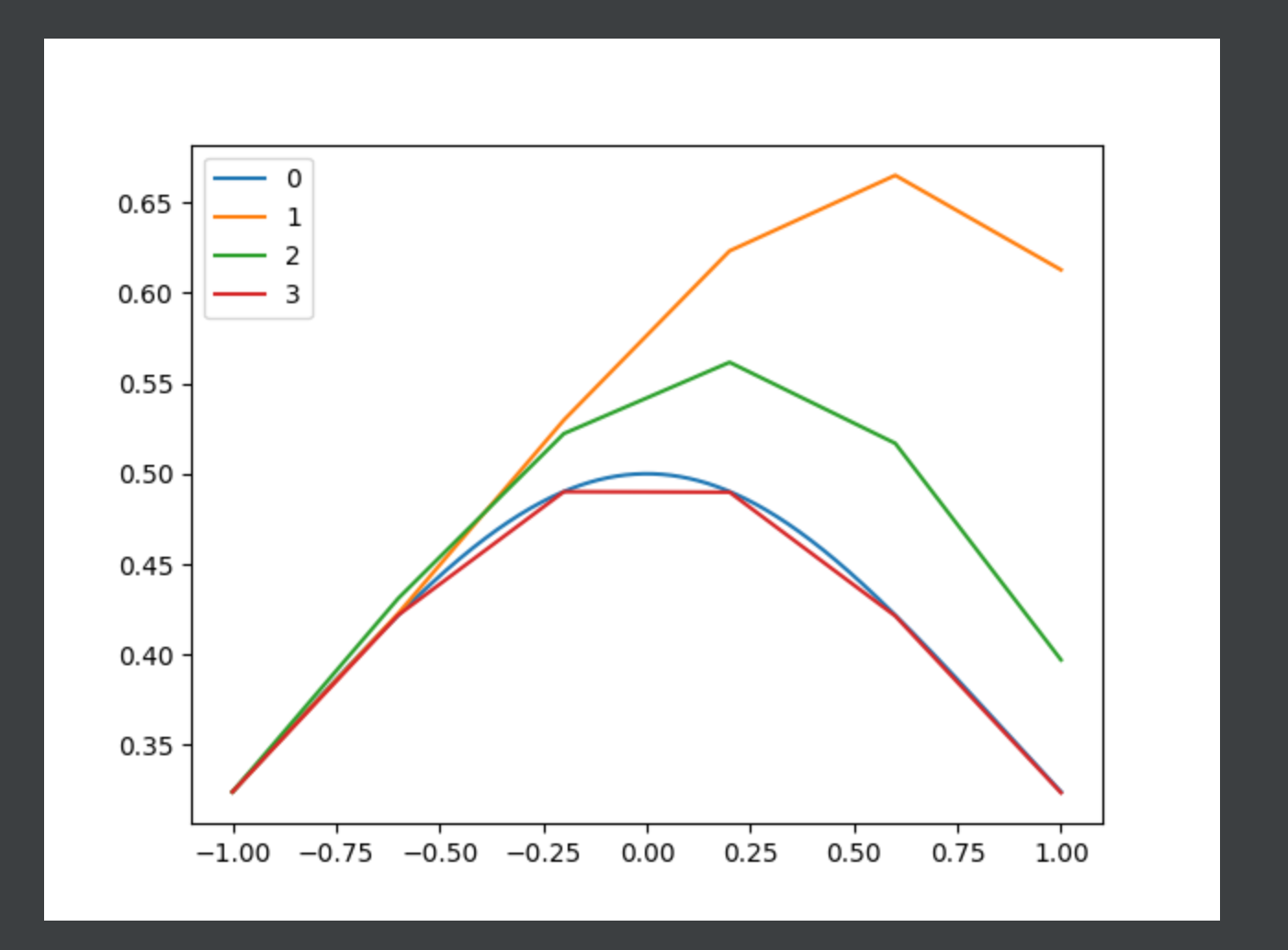
+    plt.plot(t0, r0, label='0')
+    plt.plot(t1, r1, label='1')
+    plt.plot(t2, r2, label='2')
+    plt.plot(t3, r3, label='3')
+    plt.legend()
+    plt.show()
+
+
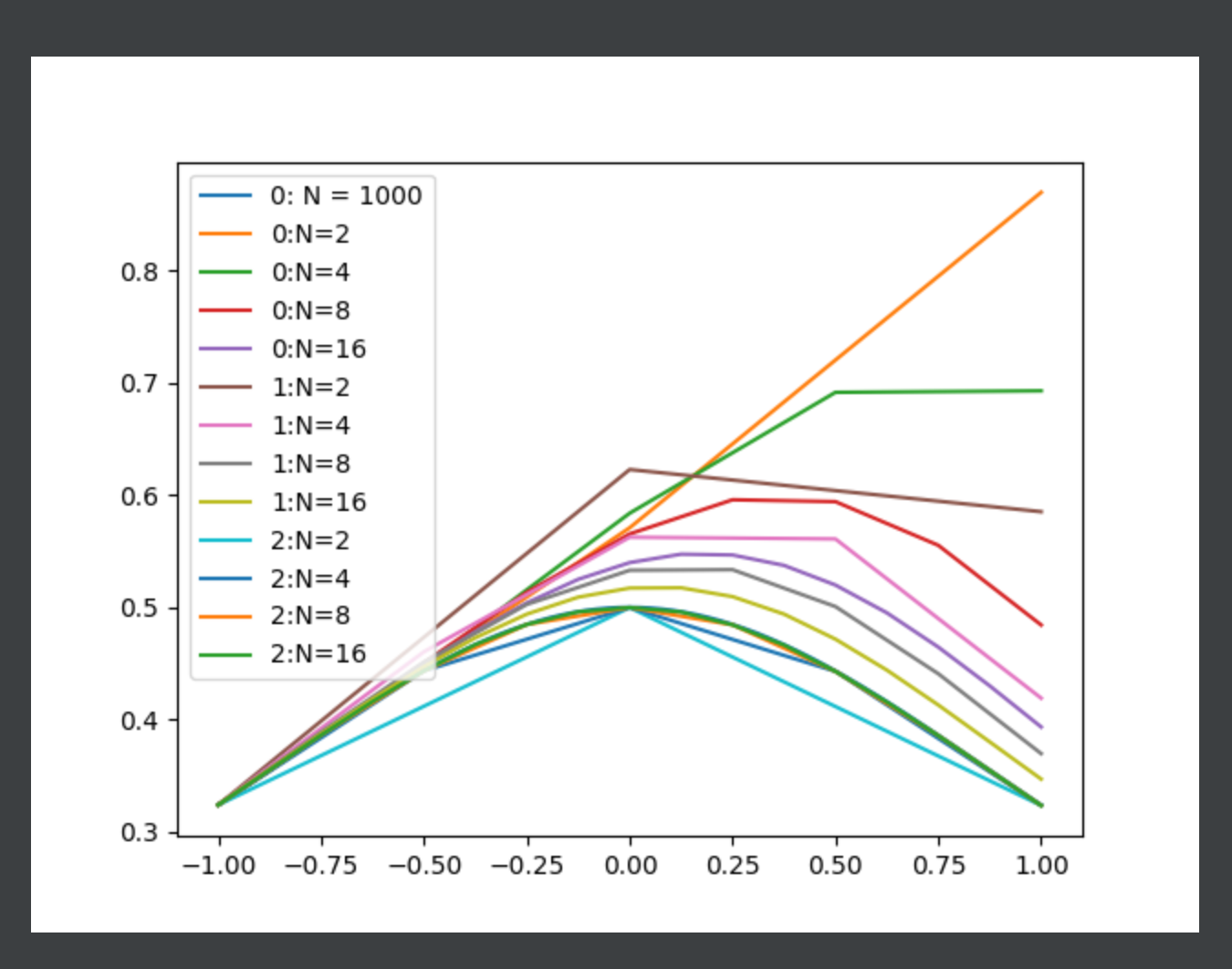
+def showN():
+    t0 = np.linspace(-1, 1, 1000)
+    r0 = solve0()
+    plt.plot(t0, r0, label='0: N = 1000')
+    solves = [solve1, solve2, solve3]
+    for j in range(3):
+        for i in range(1, 5):
+            n = 2 ** i
+            t = np.linspace(-1, 1, n + 1)
+            plt.plot(t, solves[j](t), label='%s:N=%s' % (j, n))
+    plt.legend()
+    plt.show()
+
+
+if __name__ == '__main__':
+    showN()