工程数值方法与机器学习

2020/2021 学年

北京航空航天大学微电子学院

授课教师：王鹏教授，邢炜博士

作业1

简介:

在本次作业中，你需要编写Matlab（或python）程序来求解一些线性方程组，你需要能在电脑上运行Matlab2012a以上版本（或python）。请按照本文档中的说明执行任务并生成并以所需格式保存结果。提交你的求解器代码和报告（其中包含总结和图表）。完成A部分与B部分的所有内容。

A部分：编写你自己的求解器

编写一个用来求解方程 Ux = d的向后替代求解器, 其中 U 是上三角矩阵。
编写一个方阵 A的LU分解求解器。建议添加选主元步骤，它通过交换矩阵的行来避免小数字的除法，可以有效提高稳定性。
结合（1，2）编写一个线性方程组的求解器。
编写一个Jacobi求解器。

B部分：测试你的求解器

i 对不同的bi 求解线性方程组Axi = bi ，其中A 是随机矩阵。
- 1. 创建 NxN 的随机矩阵 A. 确保 A 的行列式不接近0. 你可以通过给A加上一个对角阵来确保行列式不为零。
- 1. 创建i=1…1000 的随机向量bi
- 1. 对每个 i, 求解Axi = bi , 通过求解上面的问题并计算平方根均方误差 (RMSE, a.k.a., L2误差，计算方法为：假如解法器求得为x*，误差计算为 (Ax*-b)^2 的平均值 ). 记录每次求解的总计算时间。
- 1. 对 N =（2,4,8,16,32,64,128,…,2048 ), 比较下面几个不同的求解器的精度和消耗时间。
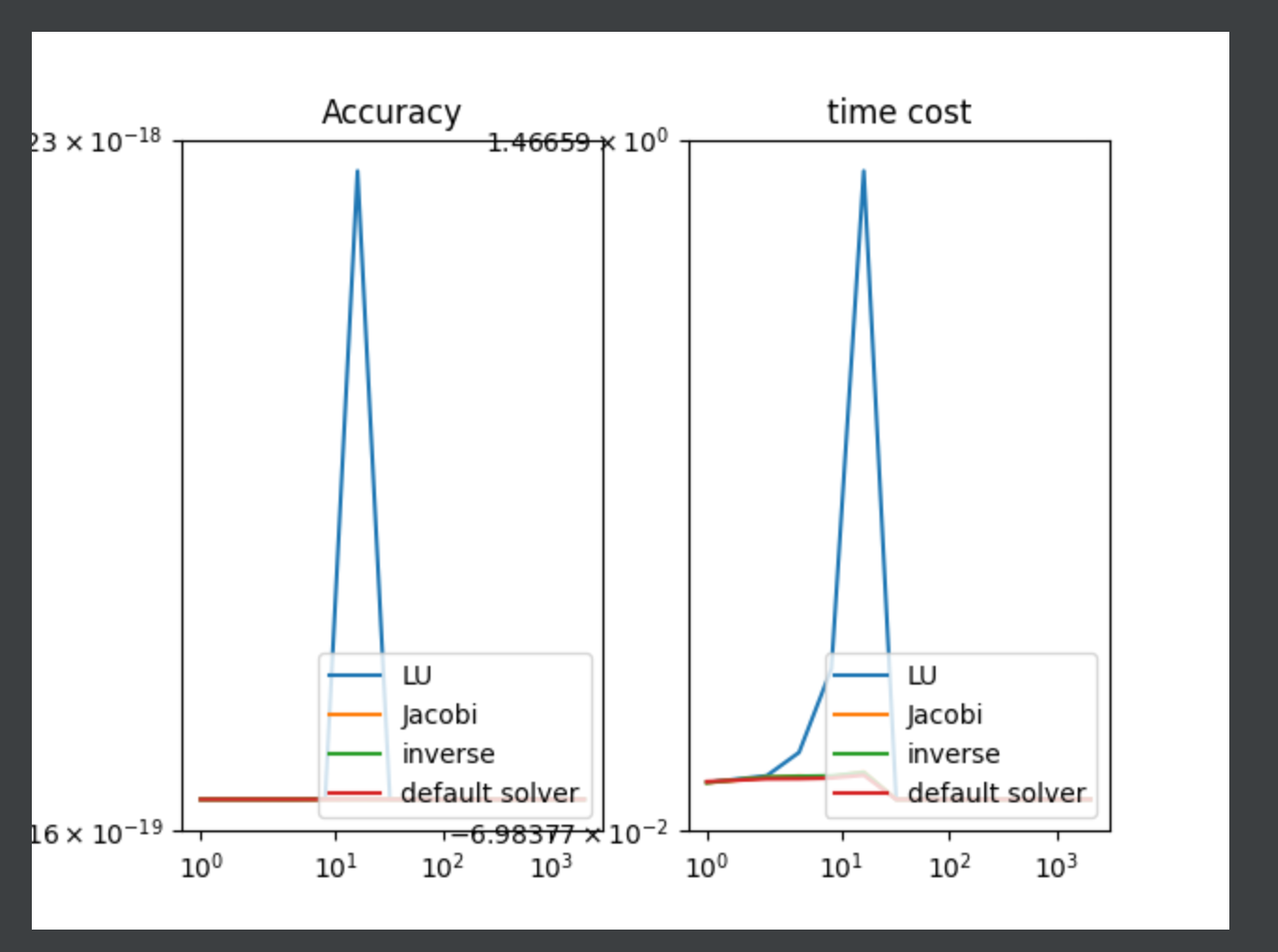
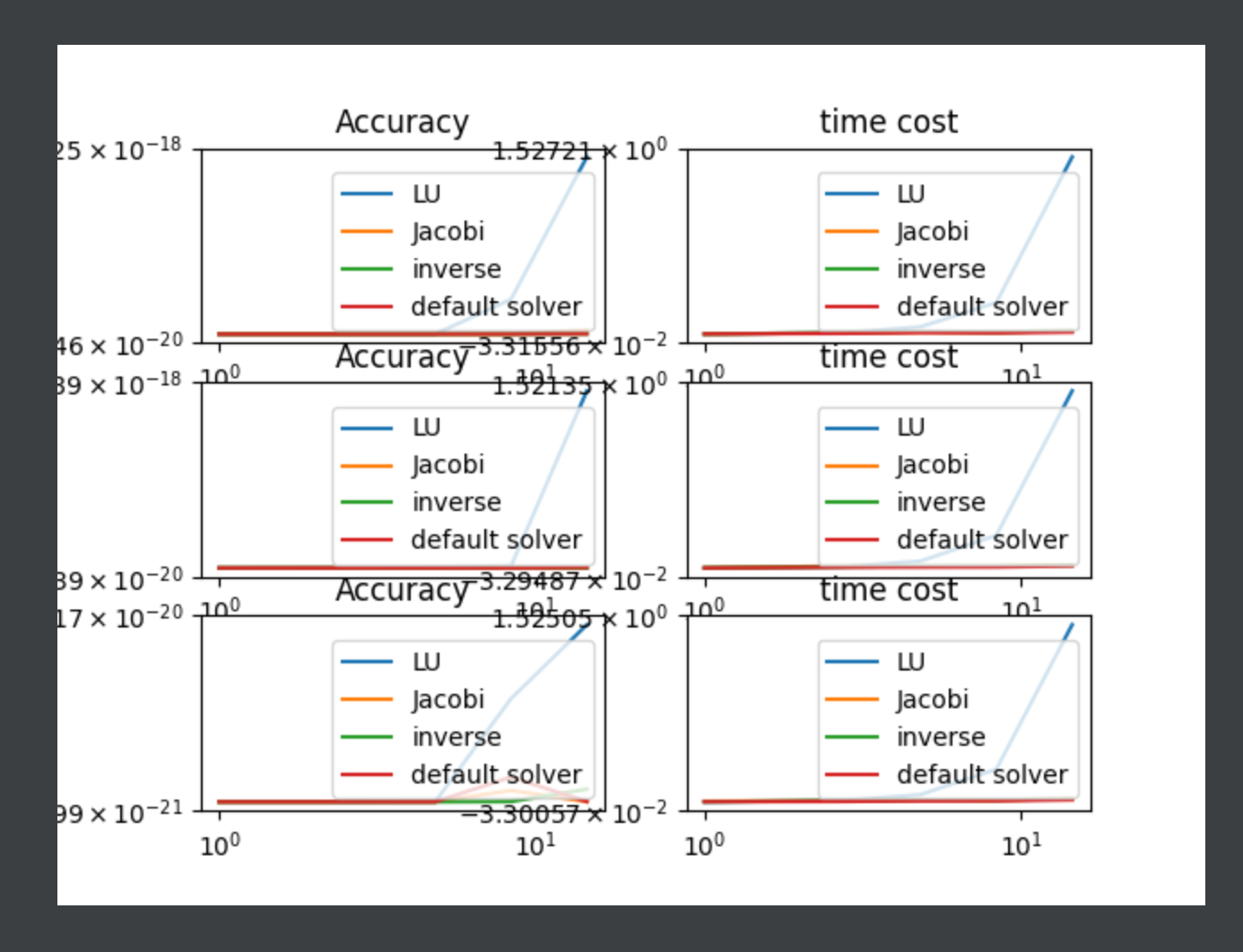
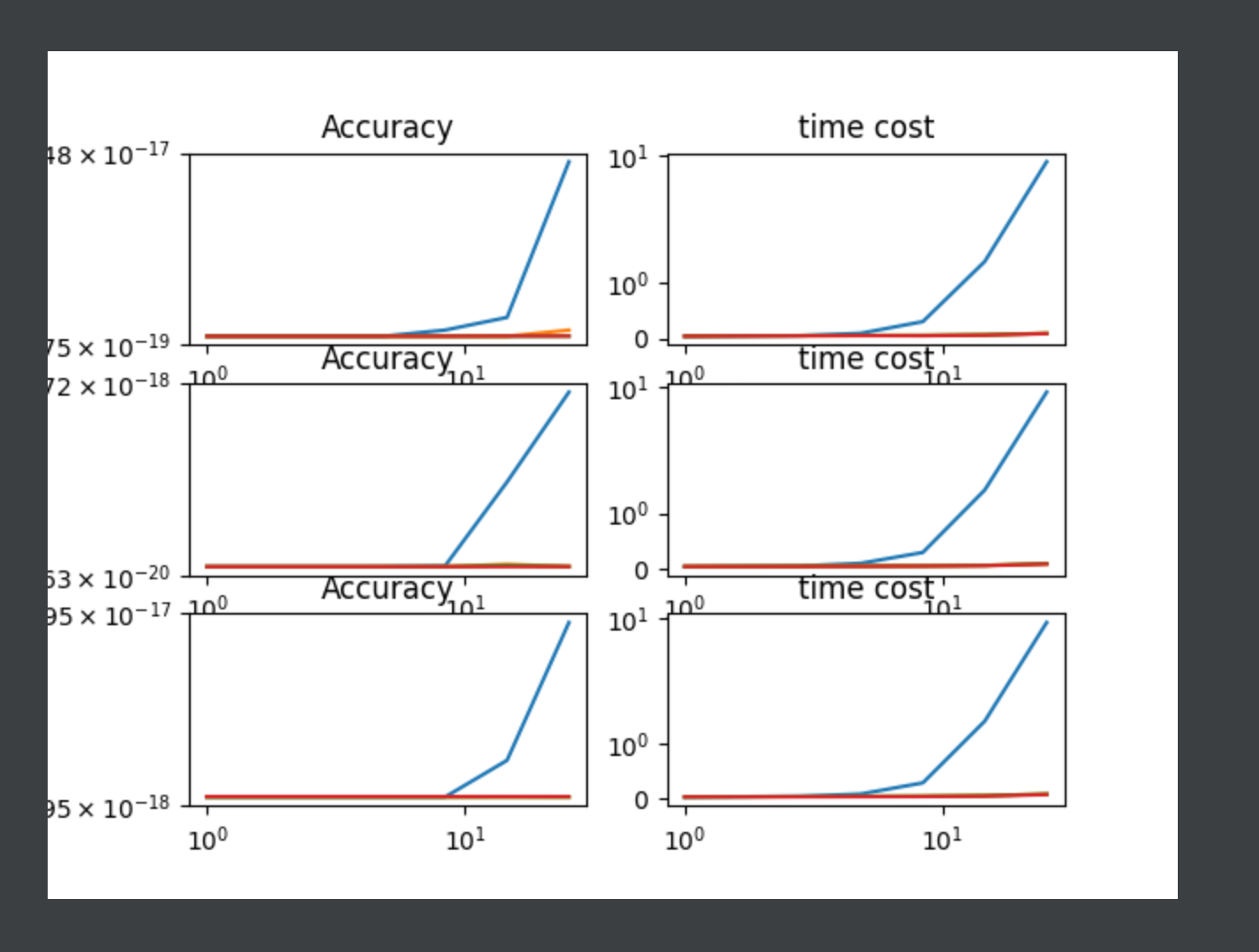
  - a. 你的基于LU分解的求解器, b. 你的Jacobi求解器 c. 对矩阵 A 求一次逆 (Matlab 命令: inv(A) or A^(-1) ) 并直接计算结果inv(A)*b d. Matlab的默认求解器 linsolve(A,B) (或者python的默认求解器). 结果应当类似下图:

(ii) 对不同的bi 求解线性方程组Axi = bi ，其中矩阵A的条件数较大。这个目标和B部分 (i) 类似，除了A被设计为病态矩阵，顾名思义，有较大的条件数 Tips: 如果你不知道怎么生成一个病态随机矩阵，可以按下面的Matlab函数来生成。你可以直接将下面的代码复制到你的Matlab程序中使用。 function A = illA(N) A = rand(N); A = (A + A') / 2;

[U,S,V] = svd(A);
S(1,1) = S(1,1) * 10^log(N^2);
S(end,end) = S(end,end) ./ 10^log(N^2);

A = U * S * V';

end

(iii) 对不同的bi 求解线性方程组Axi = bi ，其中矩阵A是随机稀疏矩阵。这个目标和B部分 (i) 类似，除了A被设计为稀疏矩阵，它的大部分元素都是0。

生成(i)，(i)，(iii)的图表并进行对比，总结你的实验结论，例如，什么情况下使用什么解法器是比较合适的；为什么Matlab自带的解法器效果总是最好等等。

作业提交有效时间是今天到10月23日（两周后）之前的任意时间。提交作业请将代码和报告打包，以“课后作业1-名字-学号”命名提交。

README.md Unescape Escape

工程数值方法与机器学习

作业1

README.md